Fractales

Un fractal es un objeto matemático con la característica de lo que llamamos autosimilaridad. Un objeto autosimilar es aquel cuya forma está generada por copias a diferentes escalas de una misma estructura. Existen diversos tipos y representaciones de fractales, pero esta hablaremos de algunos casos interesantes cuya representación se desarrolla en 2 dimensiones.

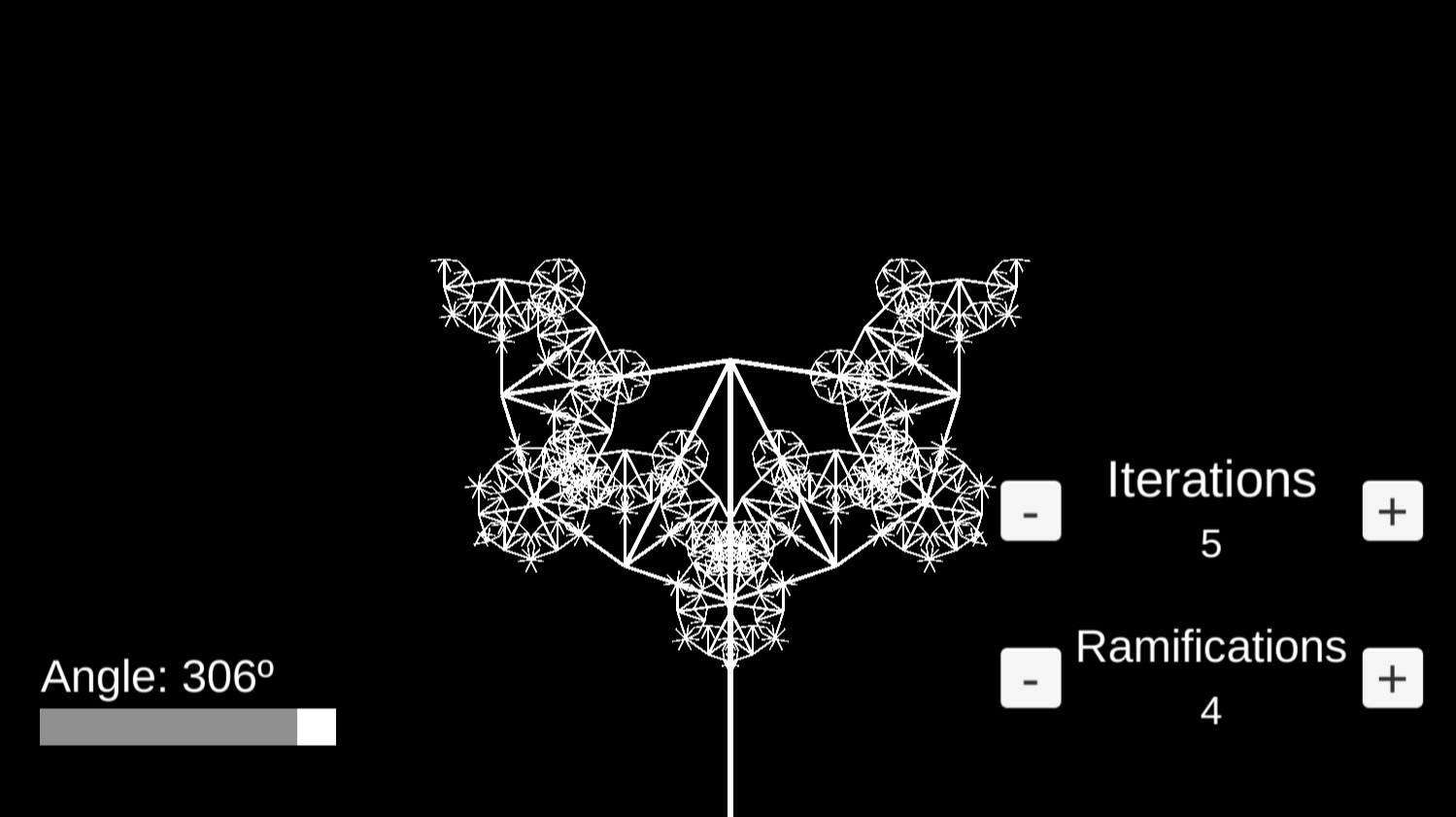
Árboles fractales

Un árbol fractal (o dosel fractal) es uno de los fractales más fáciles de generar. Para generar un dosel fractal debemos bifurcar iteradamente un segmento cumpliendo las siguientes reglas:

• Cada segmento se subdivide en un número constante de segmentos.
• El ángulo entre dos segmentos conectados al mismo segmento es constante.
• La proporción de longitud entre segmentos sucesivos es constante (normalmente 1/2).

Juego del caos

El juego del caos es un método dentro del campo de los fractales que nos permite generar estructuras autosimilares a partir de un grupo de vértices (generalmente pertenecientes a formas geométricas regulares) y un punto de inicio seleccionado aleatoriamente en el plano.

Uno de los aspectos mas interesantes de esta técnica está en que la generación de estas estructuras se realiza seleccionando vértices de forma aleatoria. Para ello, seguimos el siguiente algoritmo:

• 1: Partimos de un punto aleatorio cualquiera del plano c₀.
• 2: Elegimos como a_n a un vértice aleatorio de la figura geométrica.
• 3: Colocamos un punto en el punto medio entre c_n y a_n e iteramos nuevamente desde el paso 2 con c_n+1 éste punto medio.

Iterando este proceso obtenemos estas estructuras tan bonitas. Además de esto, podemos imponer diferentes restricciones en el paso 2 que condicionarán la figura resultante.

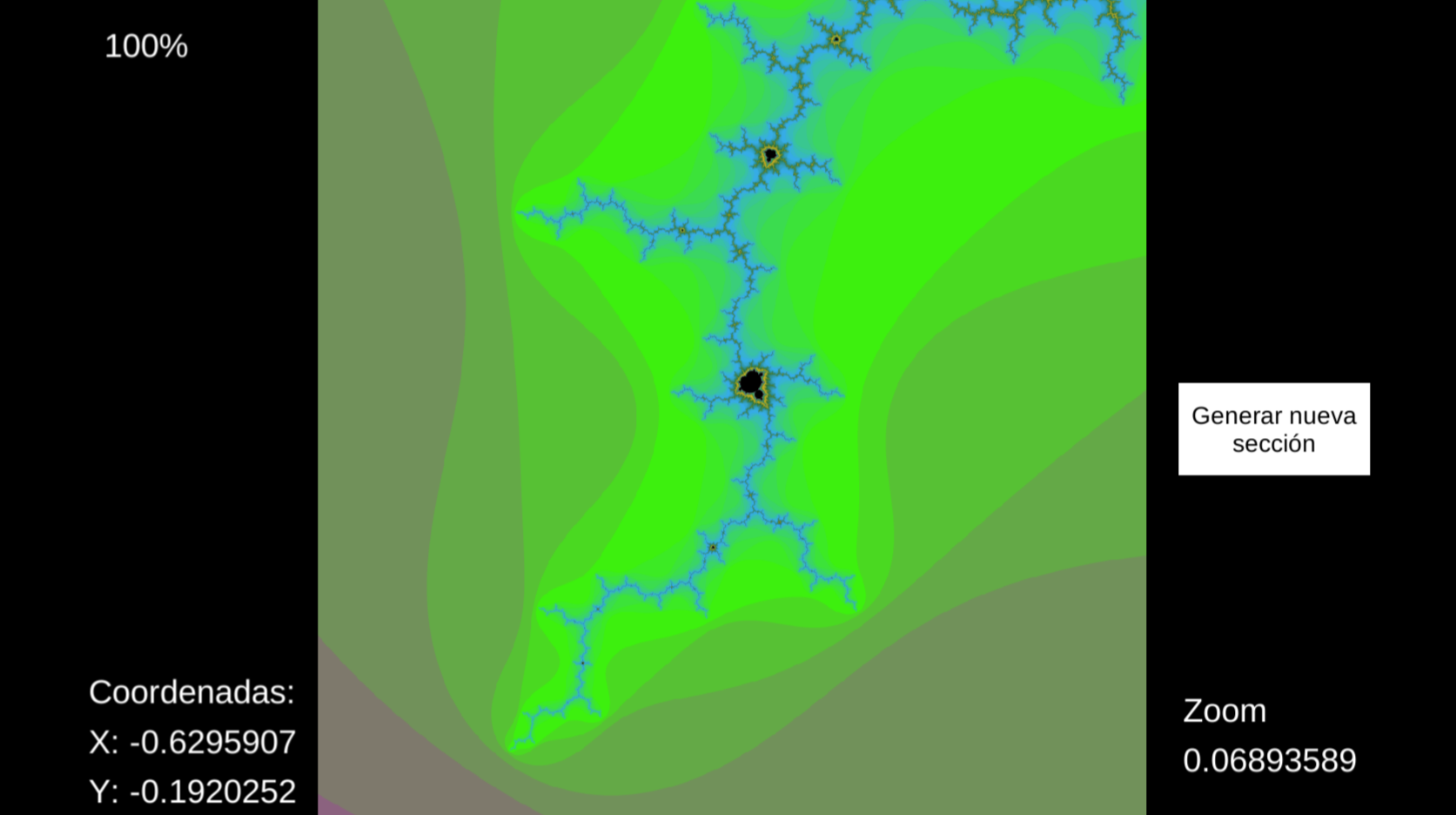
El conjunto Mandelbrot es uno de los fractales más conocidos y estudiados por los matemáticos. Un punto C pertenecerá al conjunto de mandelbrot si tras aplicarle la siguiente sucesión, su módulo es inferior a 2:

• Z₀ = C
• Z_n+1 = Z_n² + C

Si, por ejemplo, tomamos como C el valor -1, obtendremos la sucesión -1, 0, -1..., cuyo módulo nunca será mayor que 2, por lo que podemos decir que -1 pertenece al conjunto Mandelbrot. Si, en cambio, tomamos C como 1, la sucesión que obtendremos será 1, 2, 5, 26..., la cual sale del conjunto (su módulo supera a 2) rápidamente, por lo que se dice que 1 no pertenece al conjunto.

De esta forma, si realizamos este proceso con todos los puntos del plano imaginario y coloreamos aquellos pertenecientes al conjunto, obtendremos la representación deseada. Por último, cabe destacar que si asignamos un color al número de veces que hemos tenido que aplicar la sucesión a cada punto (negro si nunca sale, rojo si ha escapado a las 10 iteraciones, azul si escapa a las 100...), obtendremos una representación cromática basada en el número de iteraciones que necesita un punto para escapar del conjunto.

En la siguiente aplicación, el usuario puede seleccionar diferentes regiones del fractal de mandelbrot y observar con todo detalle su estructura.

Estas 3 aplicaciones están integramente diseñadas con Unity y programadas en C#.